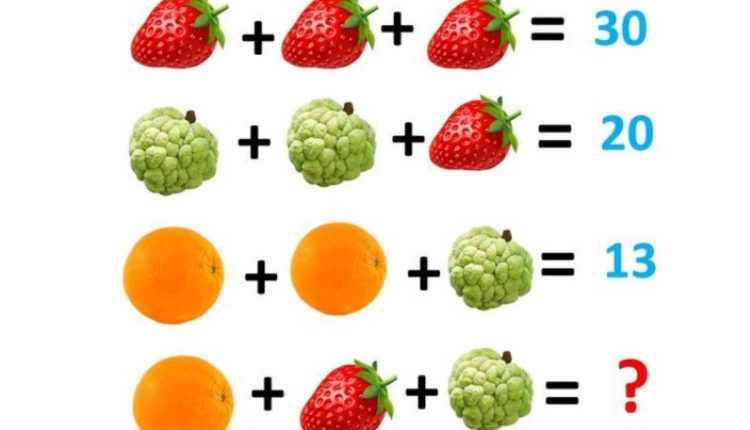
Na imagem apresentada neste desafio, há diferentes frutas se somando. Sua missão? Encontrar o valor de cada fruta e somar na última equação. Pode parecer um desafio fácil, mas aqui está o grande truque: você precisa resolver a equação em 15 segundos.
O que são desafios matemáticos
Desafios matemáticos são problemas ou quebra-cabeças que exigem a aplicação de conceitos matemáticos para serem resolvidos. Eles podem variar desde problemas simples de aritmética até problemas complexos que envolvem álgebra, geometria, cálculo, teoria dos números e mais. Os desafios matemáticos são usados tanto para entretenimento quanto para fins educacionais, ajudando a aprimorar várias habilidades cognitivas.
Tipos de Desafios Matemáticos
- Problemas de Aritmética: Questões que envolvem operações básicas como adição, subtração, multiplicação e divisão.
- Quebra-cabeças de Lógica: Problemas que exigem raciocínio lógico e pensamento crítico.
- Problemas Algébricos: Enigmas que envolvem equações e fórmulas.
- Geometria: Desafios que requerem conhecimento de formas, tamanhos, ângulos e propriedades do espaço.
- Problemas de Probabilidade e Estatística: Enigmas que lidam com a análise de dados e eventos aleatórios.
O desafio das frutas
A imagem apresenta um quebra-cabeça matemático composto por várias frutas. Existem quatro linhas com diferentes combinações de frutas e seus valores:
- Primeira linha: Três morangos somam 30.
- Segunda linha: Dois frutos do conde e um morango somam 20.
- Terceira linha: Duas laranjas e um fruto do conde somam 13.
- Quarta linha: Uma laranja, um morango e um fruto do conde, com um valor a ser descoberto.
Seu desafio é encontrar o valor individual de cada uma dessas frutas e depois descobrir o valor da quarta linha, a última equação.
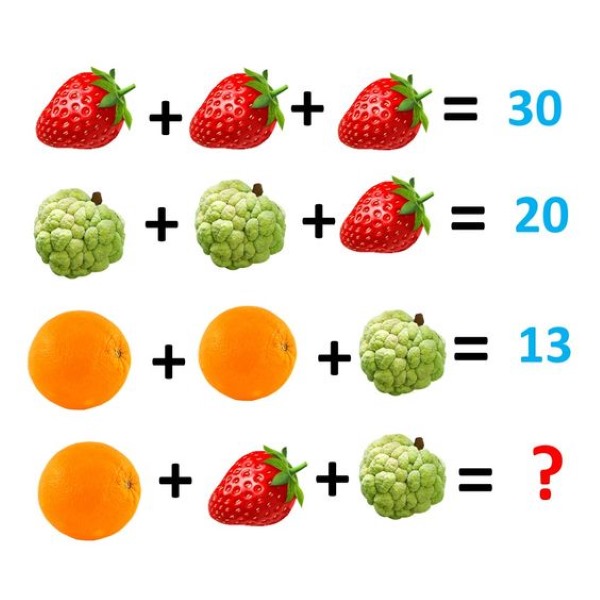
Resposta do desafio
Vamos resolver o quebra-cabeça passo a passo:
- Primeira linha: Morangos+Morangos+Morangos=30\text{Morangos} + \text{Morangos} + \text{Morangos} = 30 3M=303M = 30 M=10M = 10Portanto, cada morango vale 10.
- Segunda linha: Fruto do Conde+Fruto do Conde+Morangos=20\text{Fruto do Conde} + \text{Fruto do Conde} + \text{Morangos} = 20 Substituindo o valor do morango: 2F+10=202F + 10 = 20 2F=102F = 10 F=5F = 5Portanto, cada fruto do conde vale 5.
- Terceira linha: Laranja+Laranja+Fruto do Conde=13\text{Laranja} + \text{Laranja} + \text{Fruto do Conde} = 13 Substituindo o valor do fruto do conde: 2L+5=132L + 5 = 13 2L=82L = 8 L=4L = 4Portanto, cada laranja vale 4.
- Quarta linha: Laranja+Morangos+Fruto do Conde=?\text{Laranja} + \text{Morangos} + \text{Fruto do Conde} = ? Substituindo os valores conhecidos: 4+10+5=194 + 10 + 5 = 19
